Daniela Maftuleac, a visiting researcher at University of Ljubljana, Faculty of Computer and Information Science will be having a talk titled "Shortest path problem in rectangular complexes of global non-positive curvature". The seminar will take place on Thursday, March 13, 2014 at 12:15 in "Plemljev Seminar" room, Faculty of Mathematics and Physics, Jadranska 19.
Abstract of the talk:
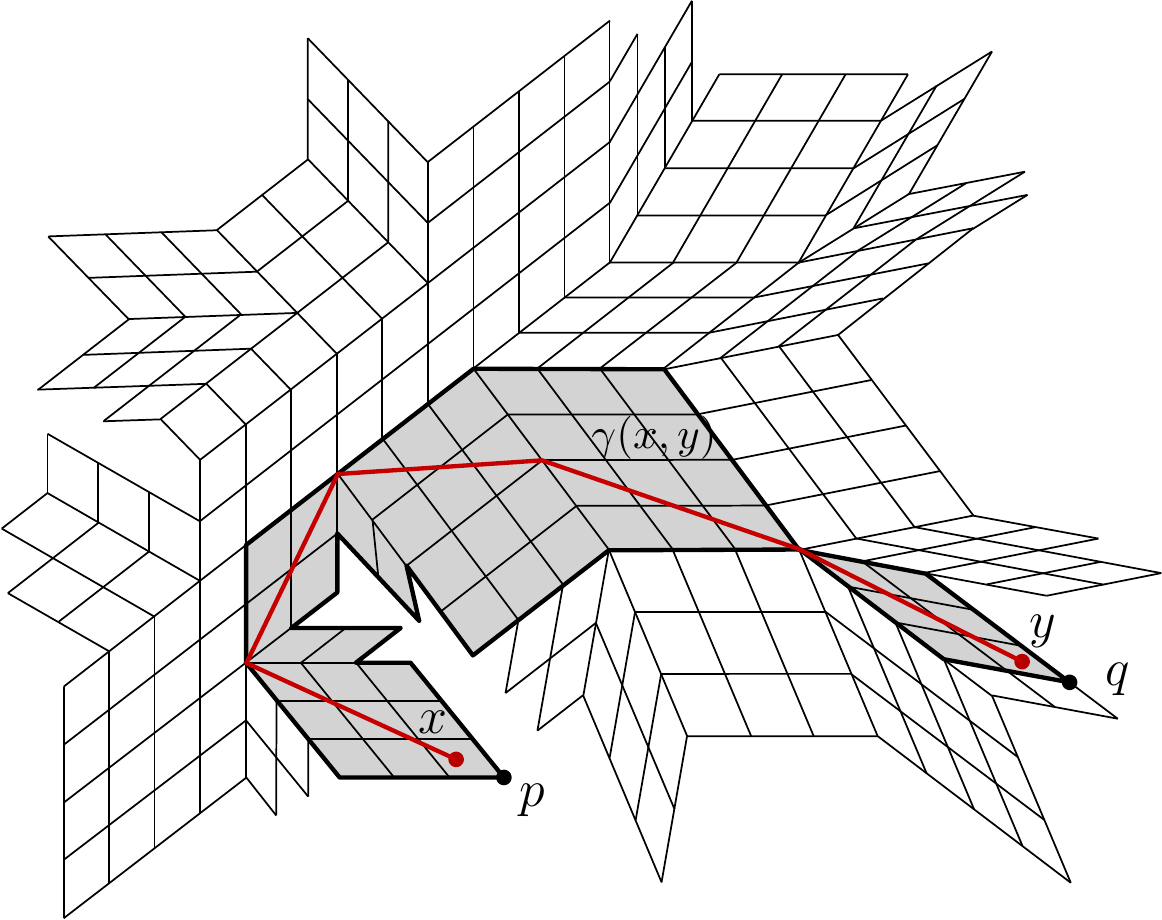
CAT(0) metric spaces (or metric spaces of global non-positive curvature) constitute a far-reaching common generalization of Euclidean and hyperbolic spaces and simple polygons: any two points x and y of a CAT(0) metric space are connected by a unique shortest path gamma(x, y).
In this talk, we present an efficient algorithm for answering two-point distance queries in CAT(0) rectangular complexes. Namely, we show that for a CAT(0) rectangular complex K with n vertices, one can construct a data structure D of size O(n^2) so that, given any two points x, y in K, the shortest path gamma(x, y) between x and y can be computed in O(d(p, q)) time, where p and q are vertices of two faces of K containing the points x and y, respectively, such that gamma(x, y) is contained in the subcomplex K(I(p, q)), d(p, q) is the distance between p and q in the underlying graph of K and I(p,q) is the interval between p and q in the underlying graph of K.