Smrtni objem

Že poznaš zgodbico o petih filozofih?

Takole gre. Za okroglo mizo sedi pet filozofov. Vsak filozof ima pred seboj krožnik s špageti, med vsakima krožnikoma pa je ena palčka. Filozofi večino časa le razmišljajo. Vsake toliko časa postane nekdo od njih lačen in poje nekaj špagetov. Špagete jedo z dvema palčkama – s palčko na svoji desni strani in s palčko, ki je na njihovi levi strani. Na mizi je skupaj le 5 palčk. Ali lahko pride do stradanja?

Kaj bi se zgodilo, če vsak filozof uporabi le palčko na svoji desni strani? Ker je filozofov pet (PROCES) in ravno toliko palčk (SKUPNI VIR), bi vsak imel le desno in nihče ne bi mogel jesti. Ubogi filozofi ne bi mogli prav dolgo razmišljati, saj bi umrli od lakote. Tak primer, pri katerem procesi drug drugega omejujejo pri pridobitvi skupnega vira, imenujemo smrtni objem (ang. deadlock). V našem primeru vsak proces potrebuje dva vira (desno in levo palčko). Ko vsi vzamejo svojo desno palčko, ne morejo več do svoje leve, saj je že v rokah prvega procesa.


Čakalna vrsta z listki

Verjetno si že kdaj bil(-a) v trgovini na oddelku delikatese ali na pošti. Kak je bil postopek razvrščanja in kako so te postregli?

Da se stranke ne sporečejo, katera je prva prišla v vrsto, je na začetku čakalne vrste avtomat s številkami, kot na spodnji sliki. Vsaka stranka vzame listek s številko in nato čaka v vrsti, dokler se na ekranu ne izpiše ustrezna številka. Tako so vse stranke zadovoljne, saj ko vzamejo listek, je navedena številka samo njihova. Transakcija jemanja listka je atomična in nihče ne more prehiteti vrste.

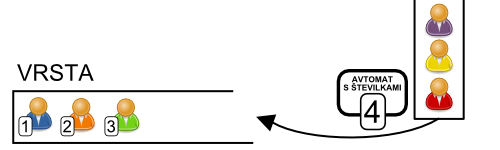
V tem primeru smo rešili problem vzporednosti s pomočjo čakalne vrste z listki, ki vključuje atomični transakciji vzami listek in stopi k okencu. V jeziku informatike imamo vmesnik (ang. buffer), v katerega lahko atomično dodamo (ang. enqueue) in iz katerega lahko atomično odstranimo (ang. dequeue) element.