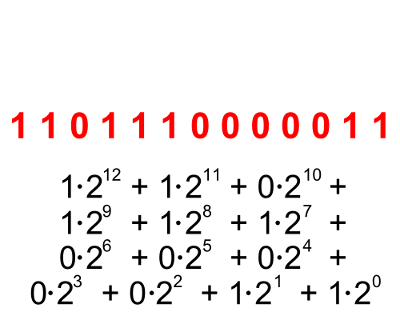Licenca
To delo je na voljo pod pogoji slovenske licence Creative Commons 2.5:
priznanje avtorstva - nekomercialno - deljenje pod enakimi pogoji.
Celotna licenca je na voljo na spletu na naslovu http://creativecommons.org/licenses/by-nc-sa/2.5/si/. V skladu s to licenco je dovoljeno vsakemu uporabniku delo razmnoževati, distribuirati, javno priobčevati, dajati v najem in tudi predelovati, vendar samo v nekomercialne namene in ob pogoju, da navede avtorja oziroma avtorje in izdajatelja tega dela. Če uporabnik delo predela, kar pomeni, da ga spremeni, preoblikuje, prevede ali uporabi to delo v svojem delu, lahko predelavo dela ponudi na voljo le pod pogoji, ki so enaki pogojem iz te licence oziroma pod enako licenco.
Desetiški zapis
Ker je v računalniku v enem od njegovih osnovih gradnikov mogoče hraniti in obdelovati le bite, mora biti vse, kar hranimo v računalniku in kar računalnik obdeluje, zapisano z ničlami in enicami. Pri tem ne smemo pozabiti, da gre samo za predstavitev na logičnem nivoju, medtem ko sta ti stanji na nivoju elektrotehnike v obliki dveh različnih napetosti. Pa si za začetek poglejmo, kako lahko zgolj z 0 in 1 zapišemo prav vsa števila, ki jih sicer že znamo zapisati v desetiškem sistemu.
Spomnimo se osnovne šole in poglejmo, kako smo se učili ugotavljati vrednosti desetiških števil. Uporabimo recimo število 7043. Gotovo ste že na prvi pogled ugotovili vrednost tega števila, ne da bi o tem kaj posebej premišljevali:
7 tisočic + 0 stotic + 4 desetice + 3 enice
Če zapišemo na malo bolj formalen način, dobimo:
7*103 + 0*102 + 4*101 + 3*100
V desetiškem sistemu je osnova deset (10) in vsaka števka ima lahko eno izmed desetih vrednosti: 0, 1, 2, 3, 4, 5, 6, 7, 8 ali 9. Položaj oziroma mesto števke v zapisu določa njeno utež. Tako ima števka na mestu 0 (skrajno desna števka) utež ena (100), števka na mestu 1 (druga z desne) ima utež 10 (101), števka na mestu 2 ima utež 100 (102) in števka na mestu 3 (tisočica) utež 1000 (103).
Dvojiški zapis
Ali bi lahko neposredno hranili desetiška števila v računalniku? Ne! Zakaj? Ker smo rekli, da ima posamezen priključek osnovnih gradnikov le dve možni vrednosti in ne deset. Zato moramo števila v računalniku zapisovati v številskem sistemu, ki ima le dve števki – v dvojiškem sistemu. V dvojiškem sistemu je osnova dve (2), vsaka števka pa ima le dve možni vrednosti (0 in 1). Prav tako kot v desetiškem sistemu bo položaj števke določal njeno utež, a razen enice ne bomo mogli govoriti o deseticah, stoticah, ...
Pa si oglejmo primer in skušajmo ugotoviti vrednost dvojiškega števila 1101110000011:
